- Get link
- X
- Other Apps
Bitwise Operators
As we know computer only understand and operates in Binary language. Bitwise Operators work bits. So, let us first understand binary language and bits in brief.
Binary language
Binary Language is also known as Machine language. As the name suggests it has only two numbers 0 and 1.The machine language converts each instruction to 0s and 1s. Each single digit is a Bit in binary. 0 is an Off bit where as 1 is an On bit. We can write a number in binary language using 4 bit, 8 bit or 16 bit or 32 bit format.
8-bits means number will be represented in binary with 8 digits.And same for 16 bit , the number is represented using 16 digits.
Example :14 in binary language is represented with 4-bit format as 1110 , but in 8 bit format it is written as 000001110. Here, each 0 is a off bit and 1 is on bit. Off means it is not playing part in formation of number, whereas On means it is.
Bit
Bit is single digit or value in machine language. 8-bits together form a Byte. 4-bits together are known as Nibble. Bit is the smallest part of language,which can't be divided.
Example:
1 0 0 1, it is a nibble it has four bits 1,0,0 and 1 respectively.
Binary Conversion
There are various format to represent numbers . We can write in decimal,hexadecimal or binary.But as to work with bitwise operators we only need to know binary so I will be explaining the binary conversion of numbers only.
In binary the base number is 2, as binary has only two digits 0 and 1.To represent a number as binary we show its base. Example: 14 in Binary is (00001110)2
There are many ways to convert the numbers in binary, but I will share the easiest and my favorite method of conversion with you.This method is very quick and easy. You don't need to do big calculations. Lets get started !
Now, we know the base number of binary language is 2. So all the digits are converted using the powers of 2.
The steps given in the image are extremely important.
The power starts from 0 so to write 8 bits it will rise till 7. If you want to convert in 4-bit you can just write the powers till 3.
Always write these two steps before converting to binary.Now we'll see an example to understand the conversion.
Example: Krishna wants to covert a number 17 to binary in the two formats 8-bit and 16-bit. But he want a simple approach,so he is asking for your help. Try to help him.
Solution:
8-bit Conversion:
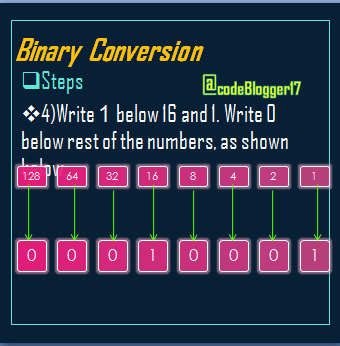
First we will write the two steps for 8-bit format ,that are shown in image above and follow the steps given below:-
1.
4.
Bravo! You did it! .The result is 00010001, its 8-bit notation of 17.
16-bit format
To covert it to 16 bit , we only need to change the step 1 and step 2.Now, instead of 0-7, we will find power from 0 to 15.
215 214 213 212 211 210 29 28 27 26 25 24 23 22 21 20
You can try it yourself. It is time consuming to find the digit in such a long format.
To covert 17 to 16 bit, we only need to insert 0's as ,we know the 16 and 1 are the bits that form 17 and they are allowed to be On bits.
215 214 213 212 211 210 29 28 27 26 25 24 23 22 21 20
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1
Hence, 17= (0000000000010001) in binary 16-bit.
Experiment: Find binary notation of 7,12,123,45,20 an 268 in 8-bit format.You can also choose any other format.You can find the number till 0-15 in 4 bit format.You won't be able to find more numbers as 4-bit format can represent 24 = 16, numbers in binary.Similarly 8-bit format can represent 28 = 256 , numbers.
Practice the binary conversion, more you practice more you understand.Stay tuned and Happy Coding!.




Comments
Post a Comment
If you have any doubt, ask here